The Evolution of Algebra, Trigonometry and Calculus in Ancient India

The Evolution of Algebra, Trigonometry and Calculus in Ancient India

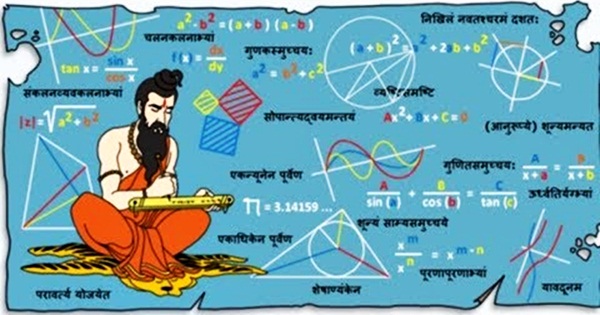
Algebra in ancient India

This is my second installation in the series of articles I proposed about the evolution of mathematics in Ancient India. In the present article, I would explore the concepts of algebra, trigonometry and calculus and their culmination in ancient India. Click here to read the first in this series.

Algebra

Quoting H.Hankel “Indeed, if one understands by the algebra the application of arithmetical operations to complex magnitudes of all sorts, whether rational or irrational numbers or space magnitudes, then the learned Brahmins of Hindostan are the real inventors of Algebra”.

Though, sophisticated geometry was invented during the origin of the Vedic rituals, its axiomatisation and further advancement was reached upon by the Greeks. The height reached by the Greeks in geometry during the period of Apolonius (260-170 BC) was unmatched by any subsequent ancient or medieval civilization. Thereafter, with the march of time the progress made in geometry reached a point of stagnation. Between the period of Pappus (300 AD) – the last big name in Greek geometry and modern Europe. Brahamagupta’s theorems (628 AD) on cyclic quadrilaterals capture the rare geniuses in the history of geometry. Further advancement needed new techniques, a completely new approach in mathematics. The new approach that followed led to the emergence and development of a new discipline- Algebra. The establishment of an algebraic culture in European mathematics during the 16^th century AD led to a renaissance in geometry through its algebraisation by Descartes and Fermat in early 17^th century. In fact, the assimilation and refinement of algebra had also set the stage for the astounding strides in number theory and calculus in Europe from the 17^th century.

Algebra was implicit in the mathematics of several ancient civilizations till it came out vividly with the introduction of literal or symbolic algebra in India. By the time of Aryabhata (499 AD) and Brahmagupta (628 AD) symbolic algebra had already evolved in India into a distinct branch of mathematics and became one of its central pillars. Evolving through various stages, algebra has now come to play a key role in modern mathematics both as an independent area in its own right as well as an indispensable tool in other branches of mathematics. Algebra provides elegance, simplicity, precision, clarity and technical power in the hands of the mathematicians. It is remarkable that the Indians had quite early realized the significance of algebra and the leading Indian mathematicians like Brahamagupta (628 AD) and Bhaskara II (1150 AD) strongly asserted the importance of their newly founded discipline.

Indians began a systematic use of symbols to denote unknown quantities and arithmetic operations. The four arithmetic operations were denoted by “Yu”, “Ksh”, “Gu” and “Bha” which are the first letters ( or a little modification) of the corresponding Sanskrit words “ Yuta” (Addition), “Ksaya” (Subtraction), “Guna” ( multiplication) and “Bhaga” ( division); Similarly “Ka” was used for “Karani” (root), while the first letters of names of different colours were used to denote different unknown variables. The introduction of symbolism was an important step in the rapid advancement of mathematics. Although, a rudimentary use of symbols can also be seen in the Greek texts of Diophantus, it is in India that algebraic formalism achieved full development.

The Indians classified and made a detailed study of equations (Known as “Sami Karana”), introduced negative numbers together with the rules for arithmetic operations including zero and negative numbers, discovered results on Surds, described solutions of linear and quadratic equations, gave formulae for geometric and arithmetic progression as well as identities involving summation of finite series, and applied several useful results on permutation and combinations including the formulae for ⁿPr and ⁿCr. The enlargement of the number system to include negative numbers was a momentous step in the development of mathematics. Owing to the early recognition of the existence of negative numbers, the Indians could give a unified treatment of the various forms of quadratic equations (with positive co-efficients), i.e., ax²+ bx=c, ax²+ c= bx, bx + c = ax². The Indians were the first to recognize that a quadratic equation has two roots. Sridharacharya (750 AD) evolved the well-known method of solving a quadratic equation by completing the square – an idea with far reaching consequences in mathematics. The Pascal’s triangle for computation of ⁿCr is described by Halayudha in the 10^th century AD as “Meru Prastara “ 700 years prior Pascal; Moreover, Halayudha’s “Meru Prastara “ was only a classification of a rule invented by Pingala more than 1200 years earlier (around 200 BC)!

Therefore, to be precise, in arithmetic, many topics in high school algebra had been systematically developed in India. This Knowledge transmitted to Europe vide the Arabs. The word “Yava” in “Aryabhatiyabhasya” of Bhaskara I (6^th Century AD) meaning “to-mix” or “to-separate” has affinity with that of “al-jabr” of al-Khwarizmi (825 AD) from which the word algebra is derived. In his widely acclaimed text on history of mathematics, Florian Cajori, a Swiss-American historian of mathematics, concludes the chapter on India with the following remarks: “…it is remarkable to what extent Indian mathematics enters into the science of our time. Both the form and the spirit of the arithmetic and algebra of modern times are essentially Indian. Think of our notation of numbers, brought to perfection by the Hindus, thinks of the arithmetical operations nearly as perfect as our own, think of their elegant algebraical methods, and then judge whether Brahmins on the banks of the Ganges are not entitled to some credit.”

Moreover, the ancient Indian algebra went far beyond the high school level. The pinnacle of Indian achievement was attained in their solutions of the hard and subtle number – theoretic problems of finding integer solutions to equations of first and second degree. Such equations are called indeterminate or Diophantine equations. But the sad part being, the Indian works in this branch were too far ahead of the times to be noticed by contemporary and subsequent civilisations! As Cajori laments, “Unfortunately, some of the most brilliant results in indeterminate analysis, found in the Hindu works, reached Europe too late to exert the influence they would have exerted, had they come two or three centuries earlier”.

Trigonometry and calculus

Beside, developing the subject of algebra proper, Indians also began a process of algebraisation and consequent simplification of other area of mathematics. For Instance, they developed trigonometry in a systematic manner, resembling its modern form, and imparted to its modern algebraic character. The algebraisation of the study of Infinitesimal changes led to the discovery of the key principles of Calculus at the time of Bhaskaracharya (1150 AD). Calculus in India reached astounding heights in the analytic trigonometry of the Kerala School in the 14^th century. Though the Greeks discovered trigonometry, their progress was halted due to absence of adequate algebraic machinery and notations. Indians invented the sine and cosine functions, discovered most of the standard formulae and identities, including the basic formula for sin (A+B), and constructed fairly accurate sine tables. Brahmagupta (628 AD) and Govindaswami (880 AD) gave interpolation formulae for calculating the sines of intermediate angles from sine tables- these are special cases of the Newton-Stirling and Newton-Gauss formulae for second – order difference. Remarkable approximations for π are given in Indian texts including 3.1416 of Aryabhata (499 AD), 3.14159265359 of Madhava (14th century AD) and 355/113 of Nilakanta (1500 AD). An anonymous work “Karanapaddhati” (believed to have been written by Putumana Somayaji in the 15^th century AD) gives the value 3.14159265358979324 which is correct up to seventeen decimal places

The Greeks had investigated the relationship between a chord of a circle and the angle it subtends at the centre- but their system is quite cumbersome in practice. The Indians realized the significance of the connection between a half – chord and half of the angle subtended by the full chord. In the case of unit circle, this is precisely the sine function. The Indian half- chord was introduced in the Arab world during the 8^th century AD. Europe was introduced to this fundamental notion through the work of the Arab scholar al- Battani (858-929 AD). The Arabs preferred the Indian half-chord to Ptolemy’s system of chords and the algebraic approach of the Indians to the geometric approach to the Greeks.

The Sanskrit word for half –chord “ardha-jya”, later abbreviated as “jya”, was written by the arabs as “Jyb”. Curiously, there is a similar sounding Arab word “Jaib” which means “heart, bosom, fold, bay or curve” when the arab works were being translated into Latin, the apparently meaningless word “jyb” was mistaken for the word “jaib” and translated as “sinus” which has several meanings in Latin including “heart, bosom, fold, bay or curve” (This word became “sine” in the English version. Aryabhata’s “Kotijya” became cosine.

The tradition of excellence and originality in Indian Trigonometry reached a high peak in the outstanding results of Madhavacharya (1340-1425) on the power series expansion of trigonometric functions. Three centuries before Gregory (1667), Madhava had described the series

θ =tan θ – (1/3)(tan θ)³ + (1/5)(tan θ)⁵ – (1/7)(tan θ)⁷+ ( |tan θ| < 1).

His proof, as presented in “Yuktibhasa” involves the idea of integration as the limit of a summation and corresponds to the modern method of expansion and term –by-term integration.

The explicit statement that (|tan θ | < 1) reveals the level of sophistication in the understanding of infinite series including an awareness of convergence. Madhava also discovered the beautiful formula

π/4 = 1 -1 /3 +1 /5 – 1/7 +

Obtained by putting θ = π/4 in the Madhava – Gregory series. This series was rediscovered three centuries later by Leibniz (1674). As one of the first applications of his newly invented calculus, Leibniz was thrilled at the discovery of this series which was the first of the results giving a connection between π and unit fractions. Madhava also described the series

π/√12 = 1-1/3.3 + 5.3²– 1/7.3³+

First given in Europe by A sharp (1717). Again, three hundred years before Newton (1676 Ad), Madhava had described the well – known power series expansions

Sin x = x-x^3/3! + x^5/5! –

And cos x = 1-x²/2! + x⁴/4! –

These series were used to construct accurate sine and cosine tables for calculations in astronomy. Madhava’s values are correct, in almost all cases; to the eighth or ninth decimal place- such accuracy was not to be achieved in Europe within three centuries. Madahava’s results show that Calculus and analysis had reached remarkable depth and maturity in India analysis had reached remarkable depth and maturity in India centuries before Newton (1642-1727) and Leibniz (1646-1716). Madhavacharya might be regarded as the first mathematician who worked in analysis!

Madhava’s contributions are mentioned in several later texts including the “Tantra Samgraha” (1500) of the great astronomer Nilakanta Somayaji (1445-1545) who gave the heliocentric model before Copernicus, the “Yuktibhasa” (1540) of Jyesthadeva (1500-1610) and the anonymous “Karanapaddhati”. All these texts themselves were discovered by Charles Whish and Published only is 1835.

Among ancient mathematicians whose tests have been found special mention may be of Aryabhata, Brahmagupta and Bhaskaracharya. All of them were astronomers as well.

Note: The above dates are according to mainstream data available. Most of our historical dates have been set by Western historians and ironically these are followed in India. According to the book Chronology of Ancient India (based on astronomical calculations, Puranas, inscriptions, and other sources) by Vedveer Arya, Brahamagupta was born in Saka 520 elapsed (63-62 BCE), which is a difference of around 700 years. Likewise, historical dates pertaining to other pre-medieval and ancient scientists, astronomers, and mathematicians have a difference of at least 500-700 years.

Featured image courtesy: YouTube.

Suggested Readings

1. F Cajori, History of Mathematics, Mac Millan, 1931.

2. Bibhutibhusan Datta, Vedic Mathematics, chap.3 of the “The cultural Heritage of India” “Vol.VI (Science and Technology)” ed. P.Ray and S N Sen, The Ramakrishna Mission institute of Culture, Calcutta.

3. B Datta and A N Singh, “History of Hindu Mathematics”, Asia Publishing House, Bombay, 1962.

4. John F Price, Applied Geometry of the Sulba Sutras in Geometry at work, ed. C. Gorini, MAA, Wahington DC, 2000.

5. T A Sarasvati Amma, Geometry in Ancient and Medieval India, Motilal Banarasidass, Delhi, 1999.

6. S N Sen and A K Bag, Post- Vedic Mathematics, Chap. 4 of “The Cultural Heritage of India Vol.VI” ed. P Ray and S N Sen, The Ramakrishna Mission institute of Culture, Calcutta.

7. S N Sen and A K Bag, The Sulbastras, INSA, New Delhi, 1983.

8. C N Srinivasiengar, the History of Ancient Indian Mathematics, the World press, Calcutta, 1967.

Acknowledgements:-

1. Late Sh. Kamalaksha Bose (Baba , You are always there in all my work).

2. Ms. Bandana Singh (tireless inspiration and support).

3. Adv. Arjun Singh (A friend and my Virgil).

4. Adv. Rajeev Pratap Singh (Guidance and support).

Facebook Comments Box